Many Muslims contend (A) Allah exists, (B) the Qur’an is divinely inspired, and (C) Muhammad split the moon.
For the sake of simplicity and explanation, let’s arbitrarily assign each of these claims a prior probability of 18%.
Now consider the following loop of reasonable premises:
P1: If Allah exists, it is more probable the Qur’an is divinely inspired.
P2: If the Qur’an is divinely inspired, it is more probable that Muhammad split the moon.
P3: If Muhammad split the moon, it is more probable that Allah exists.
Note what can happen, and very likely often does happen when there is a set of looping assumptions of this sort.
While the initial probability of the Qur’an being divinely inspired is only 18%, if we can simply assume that Allah exists, perhaps as the best explanation for the universe (see “Supplementary E”), we are then justified in bumping up the probability that the Qur’an is divinely inspired, right?
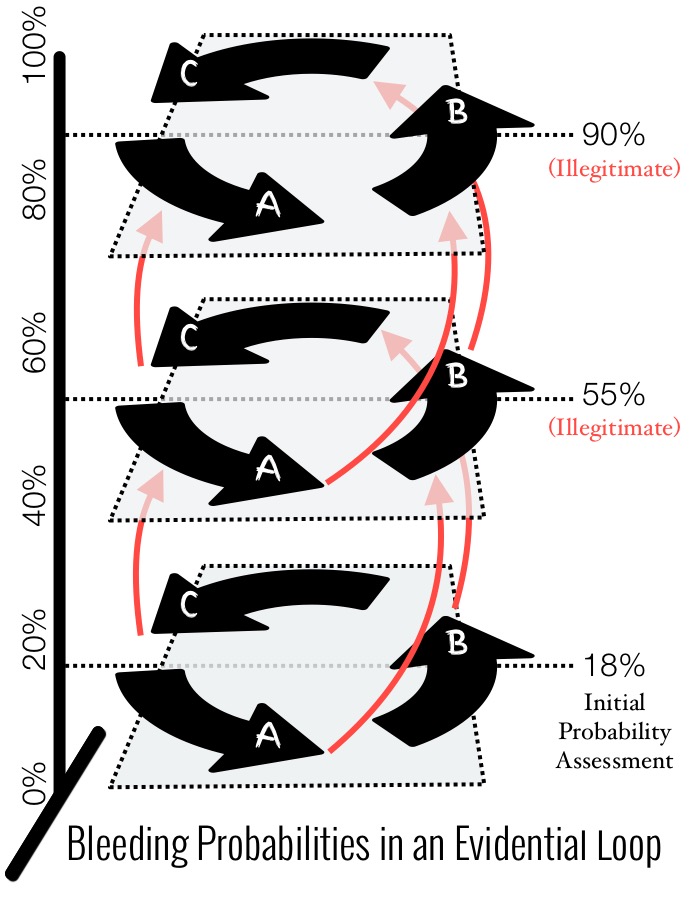
Most of us can see this leads to a circularity. If we illegitimately assume as more probably true any one of our premises originally assessed as 18% probable, that would distort the probabilities for the entire evidential loop.
Yet this seems to be a common blunder in human reasoning. The premises tend to illegitimately bleed their evidential weight upwards to the next element of the loop, that, in turn, illegitimately bleeds its evidential weight up to the next element, creating vortex ascending probabilities approaching near certainty.
These bleeding probabilities can be seen in Christianity also.
Consider the alleged resurrection of Jesus. It is often argued that, if there is (A) a true God who can resurrect, then (B) a resurrection of that God’s son becomes much more probable. And if (B) there is a resurrection of an alleged son of God, then the notion that (C) the alleged son of God is an actual son of God is increased in certainty. And if (C) the alleged son is an actual son of God, then the probability that (D) this son of God would tell the truth becomes much more probable. And if (D) the words of the biblical son of God are more probably true, then (A) a resurrecting God the biblical son of God identities is more probably the true God. And if (A) the resurrecting God is the true God, then it is more likely that (B) this God would resurrect his son. It all becomes an ascending loop of increasing certainty.
These premises are all conditional premises, and have the following combined structure:
P1: If A, B is more likely.
P2: If B, C is more likely.
P3: If C, D is more likely.
P4: If D, A is more likely.
It can be seen we have an evidential loop of four elements (A=>B=>C=>D=>A=>…). Due to our natural biases and cognitive limitations, we are inclined to wrongly allow our initial probabilities to unconsciously bleed upwards into an illegitimate higher probabilistic conclusion.
To prevent this, we need to recognize such evidential loops, and, in this awareness, rigorously anchor our probabilities to their proper positions.
This highlights the problem with making an “inference to the best explanation” as discussed in “Supplementary E”. Once the ranking of the claim against other claims as the “best explanation” becomes the focus rather than remaining anchored to the actual probability, the brain tends to loosen its probabilistic moorings on the initial assessment, and probabilities begin to bleed, yielding a higher-than-legitimate probability for every one of the elements in the loop.
Sufficient Reasons To Consider Leaving Christianity 